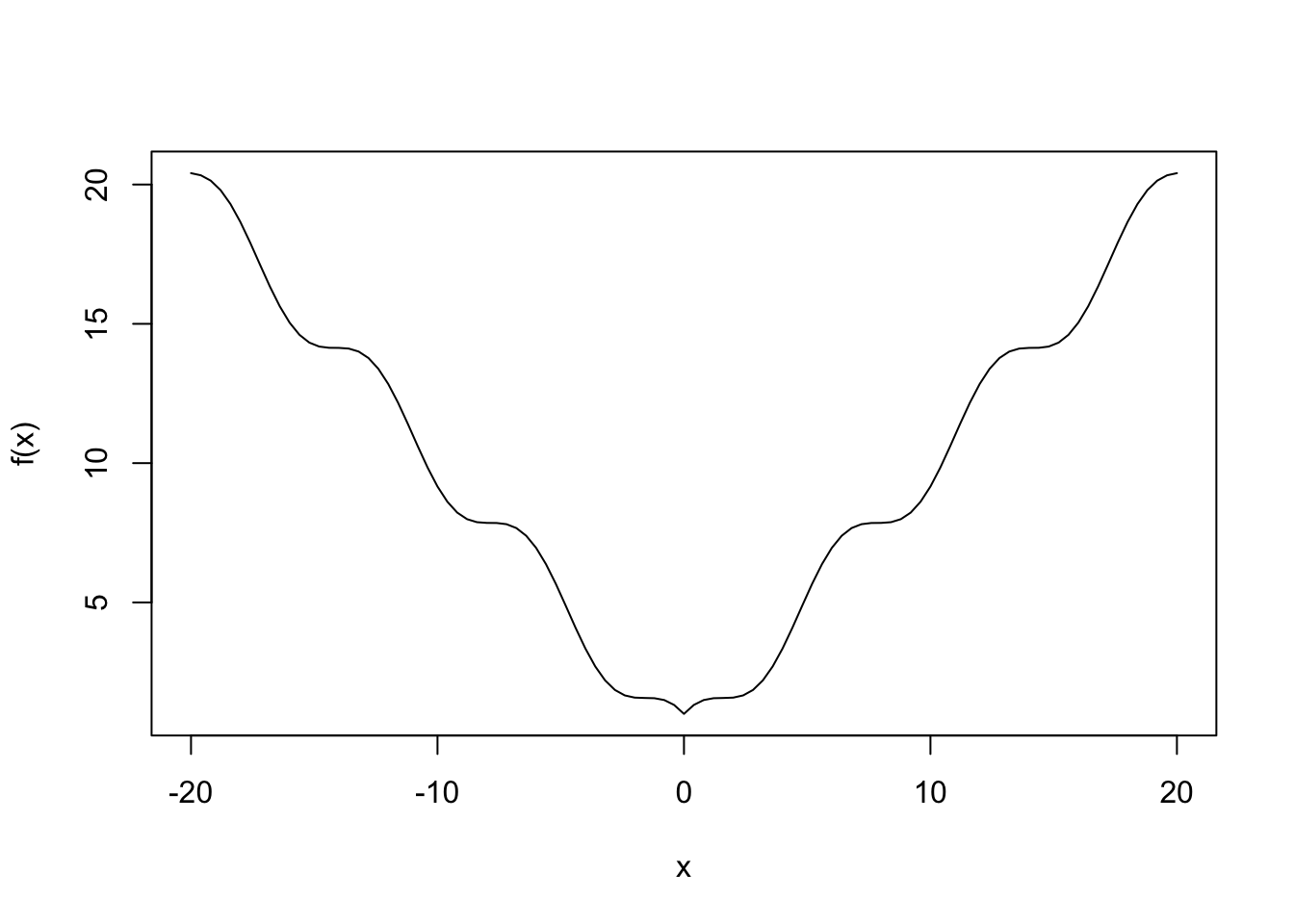
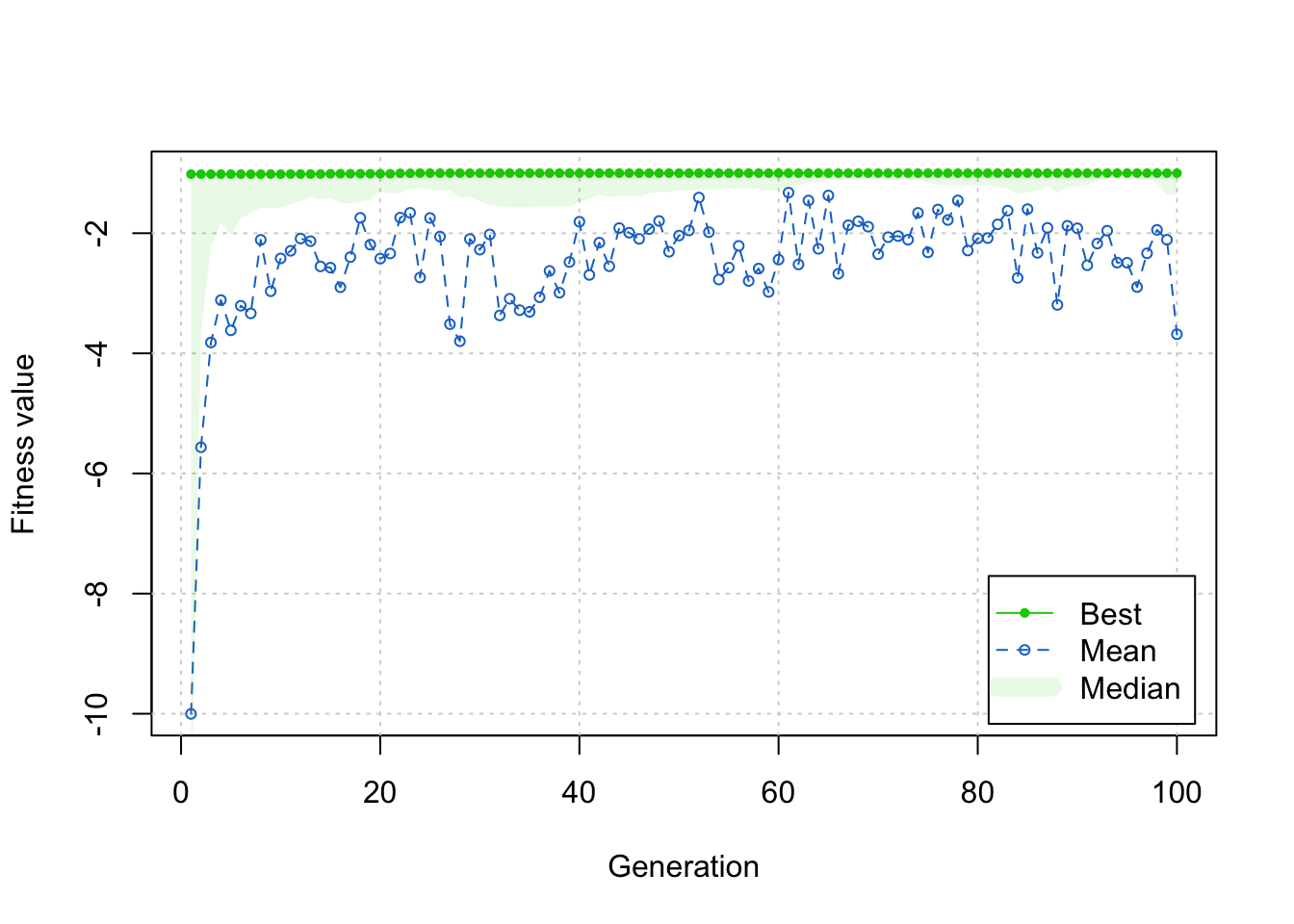
2022年3月23更新
ga(type = c("binary", "real-valued", "permutation"),
fitness, ..., # fitness:适应度函数
lower, upper, #解得下界/解得上界(多元变量为一个向量)
nBits, #一个种群用二进制编码的长度是多少(长度越大代表精度越高,一般等于变量的个数即可)
population = gaControl(type)$population, # 初始种群
selection = gaControl(type)$selection, #选择
crossover = gaControl(type)$crossover, #交叉
mutation = gaControl(type)$mutation, #变异
popSize = 50, #种群大小
pcrossover = 0.8, #交叉概率（默认0.8）
pmutation = 0.1, #变异概率（默认0.1）
elitism = base::max(1, round(popSize*0.05)), #代沟(默认情况下,前5%个体将在每个迭代中保留)
updatePop = FALSE,
postFitness = NULL,
maxiter = 100, # 最大迭代次数(默认100)
run = maxiter, #表示连续出现一定数目的目标函数值未改变,则GA终止搜索
maxFitness = Inf, # 适应度函数的上界,GA搜索后中断
names = NULL, # 表示决策变量名的向量
suggestions = NULL, # 包含某些指定的初始种群
optim = FALSE,
# optim默认值为FALSE，用于确定是否应使用使用通用优化算法的局部搜索。有关更多详细信息和更精细的控制，请参阅参数optimArgs。
# 简单理解, 即optim= T时, 表面进过一定次数的迭代后从 GA 最优解开始最为 optim函数的初始值,开始进行局部优化
# optimArgs 控制本地搜索算法的列表，具有以下组件：
optimArgs = list(method = "L-BFGS-B", # 可以是optim函数中的方法
poptim = 0.1,# 范围[0，1]中的值，指定在每次GA迭代时执行局部搜索的概率(默认值为0.1)。
pressel = 0.5,
control = list(fnscale = -1, maxit = 100)),
keepBest = FALSE, #一个逻辑参数，指定每次迭代的最佳解决方案是否应该保存在一个名为 bestSol 的槽中。
parallel = FALSE, #是否采用并行运算
monitor = if(interactive()) #绘图用的,监控遗传算法的运行状况
{ if(is.RStudio()) gaMonitor else gaMonitor2 }
else FALSE,
seed = NULL) #一个整数值包含随机数发生器的状态。这个参数可以用来复制GA搜索的结果。type: 解得编码类型
1. binary :二进制编码
2. real-valued：实数浮点编码
3. permutation：问题涉及到重新排序的列表，字符串编码。可求解TSP问题
通过gaControl设置默认的遗传算子。检索当前设置操作:
gaControl(“binary”)
gaControl(“real-valued”)
gaControl(“permutation”)函数为: $ |x|+cos(x) $
该函数有最小值$ f(0)=1（−R x R)$
rm(list = ls())
library(GA)
#> Loading required package: foreach
#> Loading required package: iterators
#> Package 'GA' version 3.2.2
#> Type 'citation("GA")' for citing this R package in publications.
#>
#> Attaching package: 'GA'
#> The following object is masked from 'package:utils':
#>
#> de
f = function(x) abs(x)+cos(x)
curve(f, -20, 20)
fitness = function(x) -f(x) #由于这个函数默认求解最大值，所以我们求-f(x)的最大值
GA = ga(type = "real-valued", fitness = fitness, lower = -20, upper = 20,monitor=F)# monitor 禁止打印信息
GA ##返回的结果GA为S4对象，一个GA类型 调用其属性用@符号
#> An object of class "ga"
#>
#> Call:
#> ga(type = "real-valued", fitness = fitness, lower = -20, upper = 20, monitor = F)
#>
#> Available slots:
#> [1] "call" "type" "lower" "upper" "nBits"
#> [6] "names" "popSize" "iter" "run" "maxiter"
#> [11] "suggestions" "population" "elitism" "pcrossover" "pmutation"
#> [16] "optim" "fitness" "summary" "bestSol" "fitnessValue"
#> [21] "solution"
GA@solution # 返回最优解
#> x1
#> [1,] -3.048778e-05
summary(GA)
#> ── Genetic Algorithm ───────────────────
#>
#> GA settings:
#> Type = real-valued
#> Population size = 50
#> Number of generations = 100
#> Elitism = 2
#> Crossover probability = 0.8
#> Mutation probability = 0.1
#> Search domain =
#> x1
#> lower -20
#> upper 20
#>
#> GA results:
#> Iterations = 100
#> Fitness function value = -1.00003
#> Solution =
#> x1
#> [1,] -3.048778e-05
## 画图--- 展示迭代信息
plot(GA) # #默认情况下，ga函数通过打印每个迭代的平均值和最佳适应度值来监视搜索,画出每代最佳的适应度函数值与每代的平均适应度函数值
# ####画出最优值
# curve(f, -20, 20) #
# abline(v = GA@solution, lty = 3)### binary 测试
GA2 = ga(type = "binary", fitness = fitness, nBits = 1,lower = -20, upper = 20,monitor=F)
GA2@solution # 返回最优解
#> x1
#> [1,] 0监视功能
xfun::pkg_load2('gifski') # 安装并加载该软件包
########################
##编写自己的跟踪功能,点代表一个解，来监视搜索
## 定义一个新的监视器函数，然后将此函数作为可选参数传递给ga:
monitor = function(obj) {
curve(f, -10, 10, main = paste("iteration =", obj@iter))
points(obj@population, obj@fitness, pch = 20, col = 2)
rug(obj@population, col = 2)
Sys.sleep(0.2)}
## 监视函数-- 运行了会输出很多静态图
# GA = ga(type = "real-valued", fitness = f, lower = -10, upper = 10, monitor = monito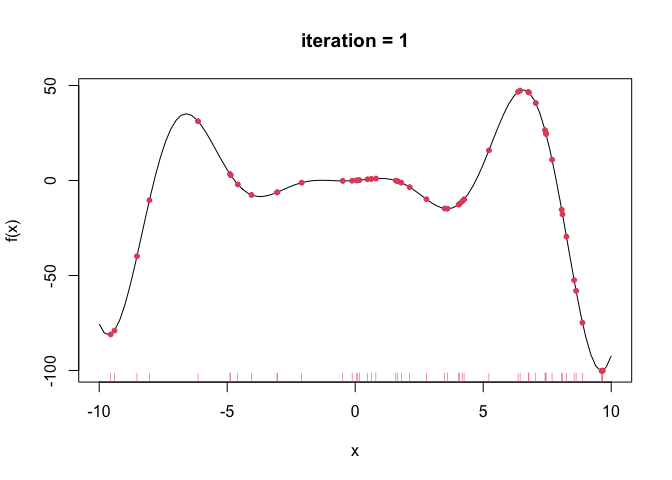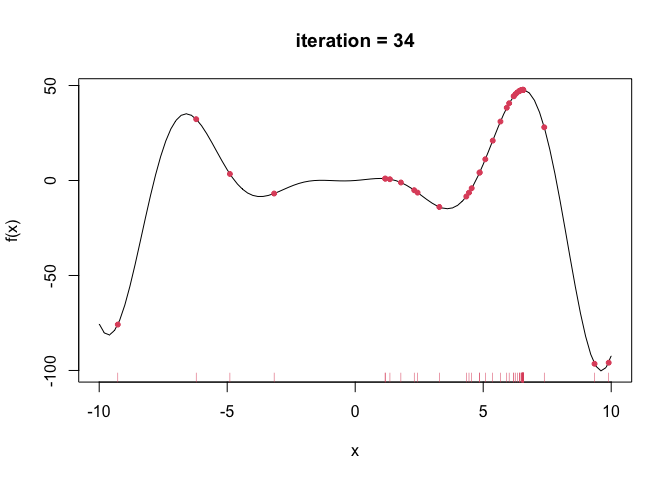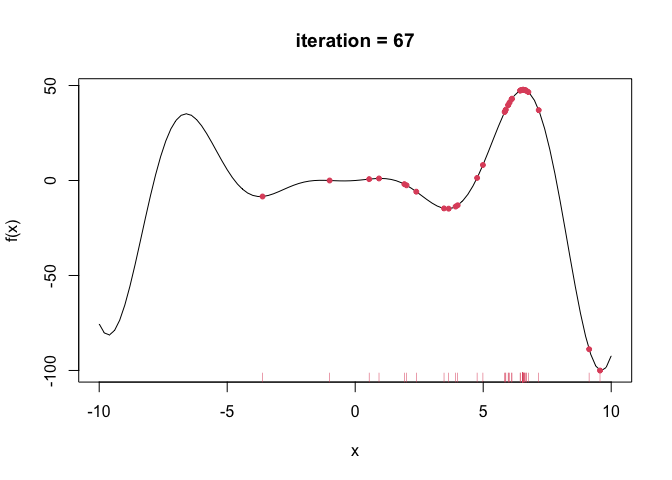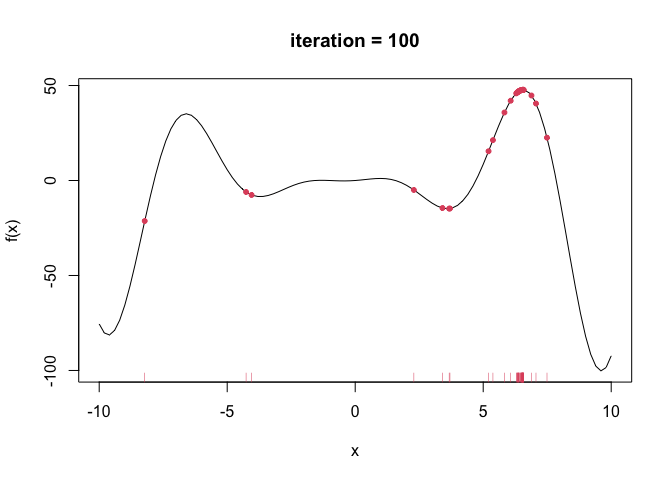r)
##############
## 也可以储存为视频，观看，利用动画的函数做出视频
# library(animation)
# oopts = ani.options(ffmpeg = "F:/ffmpeg/bin/ffmpeg.exe")#在winds中设置ffmpeg
# saveVideo({
# #打印图片
# GA = ga(type = "real-valued", fitness = f, lower = -10, upper = 10, monitor = monitor)
# ani.options(interval = 0.1, nmax = 250)
# }, video.name = "jianshi.mp4", other.opts = "-b 500k")
#
################ \[ 20 + x_1^2 + x_2^2 - 10 (\cos(2 \pi x_1) + \cos(2 pix_2)) \]
rm(list = ls())
Rastrigin = function(x1, x2) {
20 + x1^2 + x2^2 - 10 * (cos(2 * pi * x1) + cos(2 * pi * x2))
}
# 画图
# x1 = seq(-5.12, 5.12, by = 0.1)
# x2 = seq(-5.12, 5.12, by = 0.1)
# f = outer(x1, x2, Rastrigin)
# persp3D(x1, x2, f, theta = 50, phi = 20)# 3D图
# filled.contour(x1, x2, f, color.palette = jet.colors)# 热力图
monitor = function(obj) {
contour(x1, x2, f, drawlabels = FALSE, col = gray(0.5))
title(paste("iteration =", obj@iter), font.main = 1)
points(obj@population, pch = 20, col = 2)
Sys.sleep(0.2)
}
GA = ga(type = "real-valued", fitness = function(x) -Rastrigin(x[1], x[2]),
lower = c(-5.12,-5.12), upper = c(5.12, 5.12),
popSize = 50, maxiter = 100, monitor = NULL) #定义monitor,暂时不运行
GA@solution
#> x1 x2
#> [1,] -0.0001989624 1.942699e-06删除该例子
给定一组预测因子，子集选择的目的是确定最相关的预测因子，以解释响应变量的变化。我们可以利用遗传算法来赛选出更好的相关因子，从而产生更好的估计和更清晰的回归系数解释。使用二进制字符串可以自然地处理赛选子集问题，其中1表示选择该变量，0表示不选择该变量。
候选子集的适合度可以通过几种模型选择标准之一来衡量，比如AIC、BIC等
我们首先从UsingR包中加载数据集，然后通过OLS拟合线性回归模型:
rm(list = ls())
xfun::pkg_load2("UsingR")
data("fat", package = "UsingR")#252*19
mod = lm(body.fat.siri ~ age + weight + height +
neck + chest + abdomen +
hip + thigh + knee + ankle +
bicep + forearm + wrist,
data = fat)#通过观察，因变量（body.fat.siri） 与上述 13个自变量有关系
summary(mod)
#>
#> Call:
#> lm(formula = body.fat.siri ~ age + weight + height + neck + chest +
#> abdomen + hip + thigh + knee + ankle + bicep + forearm +
#> wrist, data = fat)
#>
#> Residuals:
#> Min 1Q Median 3Q Max
#> -11.1687 -2.8639 -0.1014 3.2085 10.0068
#>
#> Coefficients:
#> Estimate Std. Error t value Pr(>|t|)
#> (Intercept) -18.18849 17.34857 -1.048 0.29551
#> age 0.06208 0.03235 1.919 0.05618 .
#> weight -0.08844 0.05353 -1.652 0.09978 .
#> height -0.06959 0.09601 -0.725 0.46925
#> neck -0.47060 0.23247 -2.024 0.04405 *
#> chest -0.02386 0.09915 -0.241 0.81000
#> abdomen 0.95477 0.08645 11.044 < 2e-16 ***
#> hip -0.20754 0.14591 -1.422 0.15622
#> thigh 0.23610 0.14436 1.636 0.10326
#> knee 0.01528 0.24198 0.063 0.94970
#> ankle 0.17400 0.22147 0.786 0.43285
#> bicep 0.18160 0.17113 1.061 0.28966
#> forearm 0.45202 0.19913 2.270 0.02410 *
#> wrist -1.62064 0.53495 -3.030 0.00272 **
#> ---
#> Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
#>
#> Residual standard error: 4.305 on 238 degrees of freedom
#> Multiple R-squared: 0.749, Adjusted R-squared: 0.7353
#> F-statistic: 54.65 on 13 and 238 DF, p-value: < 2.2e-16设计矩阵(没有截距)和响应变量从拟合模型对象中提取:
x = model.matrix(mod)[, -1] # 252*13 选取13 个自变量的列，构建自变量
y = model.response(model.frame(mod)) # 提取因变量的列，
###### 那么，最大化的适应度函数可以定义为:
fitness = function(string) {
inc = which(string == 1)
X = cbind(1, x[,inc])
mod = lm.fit(X, y)
class(mod) = "lm"
-AIC(mod)
}这仅仅是利用字符串对应位置上的1所标识的预测因子来估计回归模型，并返回所选标准的负值。注意，截取项总是包含在内，并且我们使用基本的lm。拟合函数加速计算。下面的R代码运行GA:
GA = ga("binary", fitness = fitness, nBits = ncol(x),
names = colnames(x),monitor = F,parallel = T)# monitor = plot
GA@solution
#> age weight height neck chest abdomen hip thigh knee ankle bicep forearm
#> [1,] 1 1 0 1 0 1 1 1 0 0 0 1
#> wrist
#> [1,] 1
#####利用GA找到的最优子集得到的线性回归模型如下:
mod2 = lm(body.fat.siri ~ .,
data = data.frame(body.fat.siri = y, x[,GA@solution == 1]))
summary(mod2)
#>
#> Call:
#> lm(formula = body.fat.siri ~ ., data = data.frame(body.fat.siri = y,
#> x[, GA@solution == 1]))
#>
#> Residuals:
#> Min 1Q Median 3Q Max
#> -10.9757 -2.9937 -0.1644 2.9766 10.2244
#>
#> Coefficients:
#> Estimate Std. Error t value Pr(>|t|)
#> (Intercept) -22.65637 11.71385 -1.934 0.05426 .
#> age 0.06578 0.03078 2.137 0.03356 *
#> weight -0.08985 0.03991 -2.252 0.02524 *
#> neck -0.46656 0.22462 -2.077 0.03884 *
#> abdomen 0.94482 0.07193 13.134 < 2e-16 ***
#> hip -0.19543 0.13847 -1.411 0.15940
#> thigh 0.30239 0.12904 2.343 0.01992 *
#> forearm 0.51572 0.18631 2.768 0.00607 **
#> wrist -1.53665 0.50939 -3.017 0.00283 **
#> ---
#> Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
#>
#> Residual standard error: 4.282 on 243 degrees of freedom
#> Multiple R-squared: 0.7466, Adjusted R-squared: 0.7382
#> F-statistic: 89.47 on 8 and 243 DF, p-value: < 2.2e-16上述两种解决方案相比，
背包问题:假定背包的最大容量为W，N件物品，每件物品都有自己的价值和重量，将物品放入背包中使得背包内物品的总价值最大。
如果第\(i\)项选择为背包，则\(x_i = 1\)，不选则\(x_i = 0\)。考虑以下数据，利润(p)，权重(w)和容量(V):
rm(list = ls())
p = c(6, 5, 8, 9, 6, 7, 3)
w = c(2, 3, 6, 7, 5, 9, 4)
V = 14
##### 利用二进制遗传算法可以解决背包问题，但由于不等式约束，并不是所有可行解都可行。
##### 我们可以通过惩罚不可行的解决办法来考虑约束。因此，适应度函数可以定义如下:
knapsack = function(x) {
f = sum(x * p)
penalty = sum(w) * abs(sum(x * w)-V)
f - penalty
}
##### 当目标函数f被惩罚时，一个量取决于提出的解决方案的容量与背包容量之间的距离。然后:
GA = ga(type = "binary", fitness = knapsack, nBits = length(w),
maxiter = 1000, run = 200, popSize = 20)
GA@solution# 解
#> x1 x2 x3 x4 x5 x6 x7
#> [1,] 1 0 0 1 1 0 0
sum(p * GA@solution)
#> [1] 21
sum(w * GA@solution)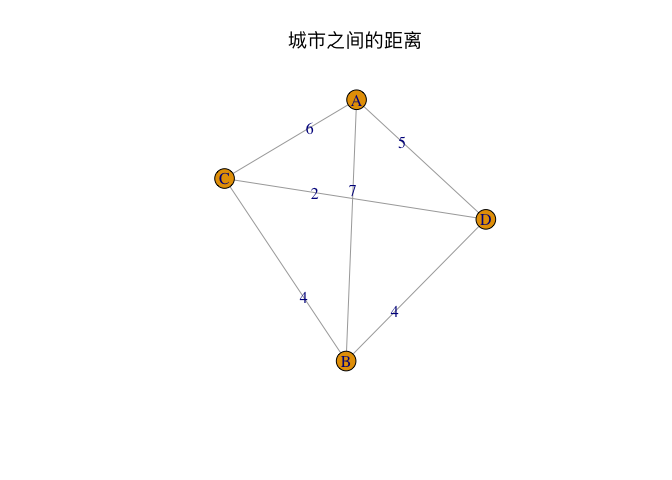
#> [1] 14有若干个城市(n个)，任何两个城市之间的距离都是确定的，现要求一旅行商从某城市出发必须经过每一个城市且只在一个城市逗留一次，最后回到出发的城市，问如何事先确定一条最短的线路。可行的解决方案的设置是由可能的途径的总数,等于(n−1)!/2.
考虑一个简单的例子，现在共有A、B、C、D四个城市。
为了将图中关系数据化，可用如下规则来描述：
城市映射为编号：A——1，B——2，C——3，D——4；
城市之间的距离用二维数组来表示，记为D[i,j]，如：D[1,2]表示城市A与城市B之间的距离，于是D[1,2]=7，同时也表示我现在处于A–1城市，将要去B–2城市； 可用遗传算法解决此类问题
rm(list = ls())
#city数据结构 一共有31个城市，计算出每两个城市之间的距离，用距离矩阵表示
D=as.matrix(dist(city)) # 距离矩阵
#定义总的路线长度
tourLength = function(tour, distMatrix) {
tour = c(tour, tour[1]) #设置为回路，代表所走的路径
route = embed(tour, 2)[,2:1]#根据回路,产生对应的距离矩阵的下标,每一行代表一个坐标，第一行处于i坐标
sum(distMatrix[route])
}
tspFitness = function(tour, ...) 1/tourLength(tour, ...)
GA3 = ga(type = "permutation", fitness = tspFitness, distMatrix = D,
lower = 1, upper = dim(D)[1], popSize = 50, maxiter = 5000,
run = 500, pmutation = 0.2,monitor = F, parallel = T)
summary(GA3)
apply(GA3@solution, 1, tourLength, D)#找到的解决方案对应于一条独特的路径，其行程长度等于:图形对比
library(ggplot2)
library(tibble)
city=rownames_to_column(city, var = "rowname")
#原始图像
# p=ggplot(data=city,aes(x=X1,y=X2))+geom_point(shape=19,size=4,col="red")+theme_bw()+
# geom_text(aes(label=rowname),size=4,vjust=1.5)+geom_path(linetype=2)+ggtitle("初始顺序")
library(dplyr)
city_solution=data.frame(solution=as.factor(GA3@solution[1,]))
re_city=inner_join(city_solution,city,by=c("solution"="rowname"))
#re_city #最优解城市顺序
##最优解城市图像
j=ggplot(data=re_city,aes(x=X1,y=X2))+geom_point(shape=19,size=4,col="red")+theme_bw()+
geom_text(aes(label=solution),size=4,vjust=1.5)+geom_path(linetype=2)+
ggtitle("最优解")+
geom_point(x=re_city[1,2],y=re_city[1,3],shape=17,size=5,col="blue")+
theme(plot.title = element_text(hjust = 0.5)) + theme(text=element_text(family="Songti SC"))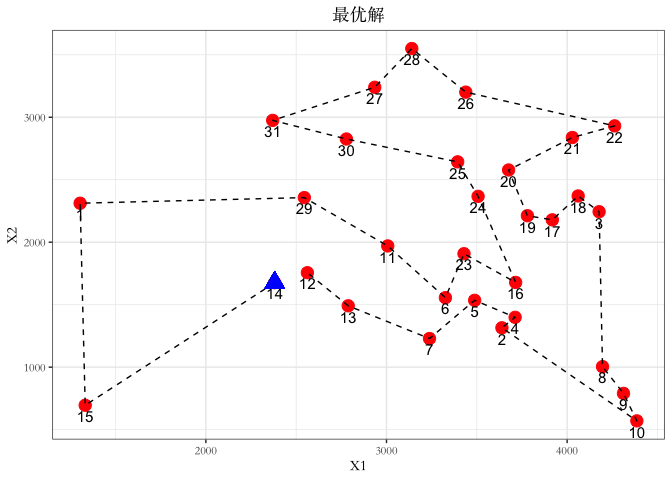
j 
sessionInfo()
#> R version 4.2.1 (2022-06-23)
#> Platform: aarch64-apple-darwin20 (64-bit)
#> Running under: macOS Monterey 12.5.1
#>
#> Matrix products: default
#> BLAS: /Library/Frameworks/R.framework/Versions/4.2-arm64/Resources/lib/libRblas.0.dylib
#> LAPACK: /Library/Frameworks/R.framework/Versions/4.2-arm64/Resources/lib/libRlapack.dylib
#>
#> locale:
#> [1] en_US.UTF-8/en_US.UTF-8/en_US.UTF-8/C/en_US.UTF-8/en_US.UTF-8
#>
#> attached base packages:
#> [1] stats graphics grDevices utils datasets methods base
#>
#> other attached packages:
#> [1] GA_3.2.2 iterators_1.0.14 foreach_1.5.2
#>
#> loaded via a namespace (and not attached):
#> [1] Rcpp_1.0.9 lattice_0.20-45 deldir_1.0-6
#> [4] png_0.1-7 assertthat_0.2.1 digest_0.6.29
#> [7] utf8_1.2.2 R6_2.5.1 backports_1.4.1
#> [10] evaluate_0.16 ggplot2_3.3.6 pillar_1.8.1
#> [13] rlang_1.0.4 data.table_1.14.2 rstudioapi_0.14
#> [16] HistData_0.8-7 gifski_1.6.6-1 UsingR_2.0-7
#> [19] rpart_4.1.16 Matrix_1.4-1 checkmate_2.1.0
#> [22] rmarkdown_2.16.1 splines_4.2.1 stringr_1.4.1
#> [25] foreign_0.8-82 htmlwidgets_1.5.4 munsell_0.5.0
#> [28] compiler_4.2.1 xfun_0.32 pkgconfig_2.0.3
#> [31] base64enc_0.1-3 htmltools_0.5.3 nnet_7.3-17
#> [34] tidyselect_1.1.2 tibble_3.1.8 gridExtra_2.3
#> [37] htmlTable_2.4.1 Hmisc_4.7-1 codetools_0.2-18
#> [40] fansi_1.0.3 crayon_1.5.1 dplyr_1.0.9
#> [43] MASS_7.3-58.1 grid_4.2.1 jsonlite_1.8.0
#> [46] gtable_0.3.0 lifecycle_1.0.1 DBI_1.1.3
#> [49] magrittr_2.0.3 scales_1.2.1 cli_3.3.0
#> [52] stringi_1.7.8 doParallel_1.0.17 latticeExtra_0.6-30
#> [55] generics_0.1.3 vctrs_0.4.1 Formula_1.2-4
#> [58] RColorBrewer_1.1-3 tools_4.2.1 interp_1.1-3
#> [61] glue_1.6.2 purrr_0.3.4 jpeg_0.1-9
#> [64] parallel_4.2.1 fastmap_1.1.0 survival_3.4-0
#> [67] yaml_2.3.5 colorspace_2.0-3 cluster_2.1.4
#> [70] knitr_1.40