matlab优化工具03全局优化之ga
首先,要明白遗传算法的基本思路,然后再利用这个函数求解问题,是非常方便的.
新版本中很多优化函数的属性设置都采用: optimoptions('优化函数', '属性1','属性值1',....)
故gaoptimset不推荐了,但是基本都差不多,可能个别参数名变了
一般模型及函数解释
\[ \begin{aligned} & \min \quad f(x) \\ & \text {s.t.} \begin{cases} \textbf{A} \cdot x \leq b \\ \textbf{Aeq} \cdot x=beq \\ c(x) \leq 0 \\ \operatorname{ceq}(x)=0 \\ l b \leq x \leq u b \end{cases} \end{aligned} \]
其中 \(f(x)\)是目标函数, \(x, b, beq\) 是向量, \(\textbf{A}, \textbf{Aeq}\)是矩阵,\(c(x)\) 和 \(ceq(x)\) 是向量函數, \(\textbf{A}\)线性不等式,\(\textbf{Aeq}\)线性等式, \(c(x)\) 非线性不等式, \(ceq(x)\)非线性等式
(求解最小值)语法:
x = ga(fun,nvars,A,b,[],[],lb,ub,nonlcon,IntCon,options)
[x,fval,exitflag,output,population,scores] = ga(___)
% 解释:
fun 为适应度句柄函数, 一般其输入为1*nvars的向量
nvars, 即目标函数自变量的个数
A,b,Aeq,beq,LB,UB,nonlcon参数与fmincon中类似,不在解释
IntCon, 整数约束, 指定变量的下标则说明该变量为整数变量
options, 算法的属性设置
x,最优解
fval, 最优解对应的目标函数值
exitflag, 算法停止的原因
output, 输出算法结构
population, 最终得到种群适应度的列向量
scores, 最终得到的种群
options = optimoptions('ga','PlotFcn',@gaplotbestf);
optimoptionsOptimization 解读, 详细解读,参考官网,这里只给出一些概念
{}里面的值为默认值{}*表示存在线性约束时的默认值,对于MutationFcn,也表示存在边界时的默认值。I*表示ga以不同方式处理整数约束的选项;;此符号不适用于gamultiobj。- NM 表示该选项不适用于gamultiobj。
- Options for
ga, Integerga, andgamultiobj
| Option | Description | Values |
|---|---|---|
ConstraintTolerance |
用以确定非线性约束的可行性, 对于选项结构,请使用TolCon。 |
Positive scalar | {1e-3} |
| CreationFcn | 建立初始种群的函数句柄 | {'gacreationuniform'} |
CrossoverFcn |
子代交叉的函数句柄 | {'crossoverscattered'} for ga, {'crossoverintermediate'}*for gamultiobj |
| CrossoverFraction | 交叉概率, 不包含由CrossoverFcn产生的子代 | Positive scalar | {0.8} |
Display |
Level of display. | 'off' |
DistanceMeasureFcn |
For gamultiobj only. 拥挤度函数 |
{'distancecrowding'} |
EliteCount |
在当前这一代种群中指定保证在下一代存活的精英个体数目 | Positive integer |{ceil(0.05*PopulationSize)} |
FitnessLimit |
NM, 如果适应度函数的值达到 FitnessLmit 的值,则算法停止 | Scalar | {-Inf} 即为一个实数,默认值 为 -lnf |
| FitnessScalingFcn | 对适应度函数的值进行缩放, gamultiobj选项不可用。 | {'fitscalingrank'} |
FunctionTolerance |
容忍度, For an options structure, use TolFun. | Positive scalar | {1e-6} for ga, {1e-4} for gamultiobj |
HybridFcn |
I* 在ga终止后继续优化的函数。指定为名称或函数句柄。 |
Function name or handle |
InitialPopulationMatrix |
初始种群. For an options structure, use InitialPopulation. |
为一个矩阵,默认值为 [ ] |
InitialPopulationRange |
初始种群的范围, 说明种群中数据元素类型的取值范围, | 取值为矩阵或向量 |
InitialScoresMatrix |
初始适应度函数的评价得分值, | 为一个列向量,默认值为 [ ] |
| MaxGenerations | 最大迭代次数 | Positive integer |{100*numberOfVariables} for ga, {200*numberOfVariables} for gamultiobj |
| MaxStallGenerations | 适应度停滞限制.当目标函数在 StallTimeLimit代后没有改 善, 则算法停止, |
{50} for ga,{100} for gamultiobj |
| MaxStallTime | 适应度停滞限制.当日标函数在 StaLlTimeLimit时间后没有改善,则算法停止, |
默认值为 lnf |
MaxTime |
算法总用时,超过后停止 | Positive scalar | {Inf} |
| MigrationDirection | 迁移方向 | 'both' |
| MigrationFraction | 从一个子种群到另一个子种群的迁移概率 | 0到1之间的数, 默认值0.2 |
| MigrationInterval | Positive integer | {20} |
|
MutationFcn |
产生变异子代的函数句柄 | {'mutationgaussian'} for ga, {'mutationadaptfeasible'}* forgamultiobj |
NonlinearConstraintAlgorithm |
非线性约束算法 | {'auglag'} for ga, {'penalty'} for gamultiobj |
OutputFcn |
ga 在每次迭代中调用的函数, | 取值为 @gaoutpulgen 或 [J(默认值〉 |
ParetoFraction |
仅用于gamultiobj, 保留帕累托解的比例? | Scalar | {0.35} |
| PlotFcn | 边计算边绘制数据 | ga or gamultiobj: {[]} | 'gaplotdistance' | 'gaplotgenealogy' | 'gaplotselection' | 'gaplotscorediversity' |'gaplotscores' | 'gaplotstopping' | 'gaplotmaxconstr' |Custom plot functionga only:‘gaplotbestf’ |
PopulationSize |
种群的数量 | Positive integer | {50} when numberOfVariables <= 5, {200}otherwise |
PopulationType |
种群中数据元素类型的字符串 | ‘bitstring’|‘custom’|{‘doubleVector’} |
SelectionFcn |
选择句柄函数,用以选择进行交叉和变异的父代 | {'selectionstochunif'} for ga, {'selectiontournament'} forgamultiobj |
UseParallel |
并行计算 | true |
| UseVectorized | 指定函数是否向量化, For an options structure, use Vectorized with the values 'on' or 'off'. |
true| {false} |
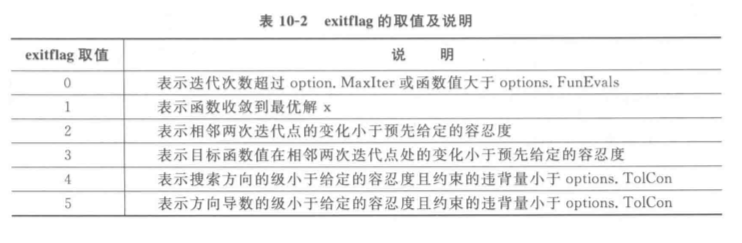

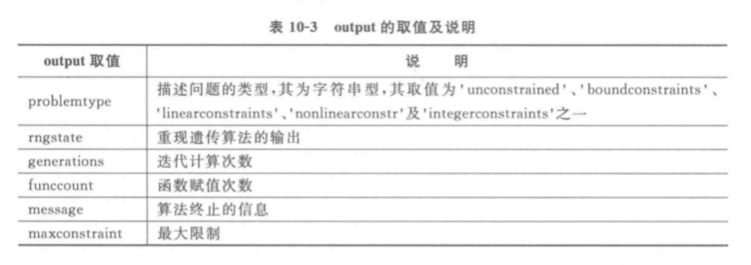
- 可以通过输出 output 参数, 来设置算法参数
例1:
\[ min \quad g(x) = (x_1 -10)^3 + (x_2 -20 )^3 \\ s.t. \begin{cases} (x_1 - 5)^2 + (x_2 - 5)^2 \geq 100\\ 13\leq x_1 \leq 100 \\ 0 \leq x_2 \leq 100 \end{cases}\\ 已知的最优点和最优值 g(x^*) = g(14.095,0.84296) = -6961.81381 \]
clc,clear all;
A = [];
b = [];
Aeq = [];
beq = [];
lb = [13,0];
ub = [100,100];
nvars = 2;
options = optimoptions('ga','Display','final','PlotFcn','gaplotbestf','FunctionTolerance',1e-6);
[x,fval] = ga(@myobjfun2,nvars ,A,b,Aeq,beq,lb,ub,@constrain,options)
%% 目标函数
function f = myobjfun2(x)
f = (x(1) - 10)^3 + (x(2) - 20)^3;
end
%% 非线性约束
function [c, ceq] = constrain(x)
% 非线性不等式约束
c = 100 - (x(1) - 5)^2 - (x(2)-5)^2;
% 非线性等式约束
ceq = [];
end结果如下:
Optimization terminated: average change in the fitness value less than options.FunctionTolerance
and constraint violation is less than options.ConstraintTolerance.
x =
13.6602 0.0000
fval =
-7.9509e+03不知道为什么? 居然比上面给出的结果还要好. 上题来源于 <<智能优化算法及其应用(王凌著).pdf>>第一章绪论 第8页 — — 第6个函数
参考:
《MATLAB R2015b最优化计算》–李娅
https://www.mathworks.com/help/gads/ga.html