matlab优化工具01线性规划之linprog
常用这些函数, 写个笔记
matlab 优化工具箱函数
基本函数

全局优化函数
- 遗传算法 ga() , 推荐, 可以处理带有约束问题的优化, 还可以求解混合整数规划
- 模式搜索算法 patternsearch()
- 模拟退火求解 simulannealbnd()
- 粒子群算法 particleswarm
基本选项参数
- optimset 函数用于获取 MATLAB 优化工具箱所有的属性设置选项
%% 函数用法与解释
options = optimset('paraml',vaJuel,'param2',value2,...) % 如果选择用系统的默认值,则只需将参数的值设为 \[\].
optimset: 列出一个完整的优化参数列表及相应的可选值。
options = optimset : 创建一个名为 optoptionslOns 的优化参数结构体,其成员参数的取值为系统的默认值。
options = optimset(optimfun): 创建一个名为 options 的优化参数结构体,其所有参数名及值为优化函数 optimfun 的默认值。
options=optimset(oldopts, 'paraml' ,valuel ,...) :将优化参数结构体 oldopts中的参数 paraml 改为 valuel 并将更改后的优化参数结构体命名为 options
options = optimset(oldopts,newopts): 将已有的优化参数结构体 oldopts 与新的 优化参数结构体 newopts 合井, newopts 中的任意非空参数值将覆盖 oldopts 中的相应参数值。
%% eg: 列出所有的优化参数列表
>> optimset
%% 结果省略- optimget 函数: 想查看某个优化参数的值
%%
val= optimget(options, 'param' ) : 获取优化参数结构体 options 中参数 param 的值。
val = optimget(options, 'param', default): 如果参数 param 在 options 中没有定义,则返回其默认值
%% eg: 查看某个优化参数的值
clc,clear all;
options = optimset('fmincon') % 省略结果
options =optimset(options, 'Display' , 'iter') %修改 Display 属性值为iter
val = optimget(options,'Display') % 重新获取fmincon 函数的 Display属性值
线性规划的标准型
\[ \begin{aligned} & \min \quad f^T x \\ & \text {s.t.} \begin{cases} \textbf{A} \cdot x \leq b \\ \textbf{Aeq} \cdot x=beq \\ lb \leq x \leq ub \end{cases} \end{aligned} \] 其中 \(f^T, x, b, beq\) 是向量, \(\textbf{A}, \textbf{Aeq}\)是矩阵,\(\textbf{A}\) 线性不等式, \(\textbf{Aeq}\) 线性等式,
matlab 实现线性规划 — linprog
% 语法
x = linprog(f,A,b,Aeq,beq,lb,ub,options)
x = linprog(problem)
[x,fval,exitflag,output,lambda] = linprog(___)
%% 如果不存在某个约束或变量,设置为空即可例1 线性规划
\[ \begin{aligned} min \quad f(x) = -5x_1 - 4x_2 - 6x_3 \\ s.t. \begin{cases} x_1 - x_2 + x_3 \leq 20\\ 3x_1 + 2x_2+4x_3 \leq 42\\ 3x_1+2x_2 \leq 30\\ x_1,x_2,x_3 \geq 0 \end{cases} \end{aligned} \]
%% matlab 实现 --- 方法一
clc, clear all;
f = [-5; -4; -6]; % 列向量
A = [1,-1,1;
3,2,4;
3,2,0];
b = [20;42;30]; % 列向量
lb = zeros(1,3); % 行向量
ub = []; % 为空,则表示无上限,即正无穷
options = optimoptions('linprog','Algorithm','dual-simplex','Display','iter');
[x,fval,exitflag,output,lambda] = linprog(f,A,b,[],[],lb,ub,options)
% ------------------ 结果 ------------------
x =
0
15.0000
3.0000
fval =
-78
exitflag =
1%% 方法二: 以结构体方式创建
%%
% optimproblem('ObjectiveSense','max') % 最优化问题的创建, ObjectiveSense属性求最大值(默认最小值)
%% optimvar 决策变量的定义,n,m,k 设置决策变量的维度,不设置k则变量维度为n*m
% x = optimvar('x',n,m,k,'LowerBound',lb,'UpperBound',ub)
prob = optimproblem('ObjectiveSense','min');
x = optimvar('x',3,1,'LowerBound',[0;0;0]);
prob.Objective = -5*x(1) - 4*x(2) -6*x(3);
prob.Constraints.c1 = x(1) - x(2) + x(3) <= 20;
prob.Constraints.c2 = 3*x(1) + 2*x(2) + 4*x(3) <= 42;
prob.Constraints.c3 = 3*x(1) + 2*x(2) <= 30
sols = solve(prob)
x0 = sols.x
% ------------------ 结果 ------------------
x0 =
0
15.0000
3.0000双下标的线性规划问题 — 运输问题
如果目标函数以及约束条件中的变量是以矩阵描述,则按照一一对应规则变成向量的形式即可求解
有些时候书写比较麻烦,比如运输问题, 则可以编写函数使其自动化

image-20210516105838325
function [x,f0, flag] = transport_linprog(C,s,d,indkey)
[m,n] = size(C); A=[]; B =[];
for i = 1:n
Aeq(i,(i-1)*m+1:i*m) =1;
end
for i = 1:m
Aeq(n+i,i:m:n*m) =1;
end
xm = zeros(1,n*m);
f= C(:);
Beq=[s(:);d(:)];
if nargin == 3
[x,f0,flag] = linprog(f,A,B,Aeq,Beq,xm);
else
[x,f0,flag] = intlinprog(f,indkey,A,B,Aeq,Beq,xm);
x = round(x);
end
x = reshape(x,m,n); %将向量解还原为矩阵所需的形式
end%% 例题
C = [464,513,654,867;
352,416,690,791;
995,682,388,685];
s = [80,65,70,85];
d=[75;125;100];
[x0,f0] = transport_linprog(C,s,d)
% ------------------ 结果 ------------------
Optimal solution found.
x0 =
0 20 0 55
80 45 0 0
0 0 70 30
f0 =
152535特殊的运输问题 — 指派问题
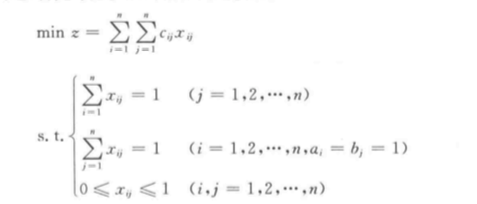
C= [15,18,21,24;
19,23,22,18;
26,17,16,19;
19,21,23,17]
s = [1,1,1,1];% s和d向量可以是列向量也可以是行向量
d = [1,1,1,1];
[n,m] = size(C);
[x0,f0] = transport_linprog(C,s,d,1:n*m)
% ------------------ 结果 ------------------
x0 =
0 1 0 0
1 0 0 0
0 0 1 0
0 0 0 1
f0 =
70参考:
matlab函数官网
<<薛定宇教授大讲堂卷5 MATLAB最优化计算>>_含目录py.pdf
<<MATLAB R2015b最优化计算—李娅>>_含目录
<<MATLAB优化算法_张岩,吴水根著_北京:清华大学出版社>>